Suis-je bien proportionné(e)?

Avouons-le: chacun(e) d'entre nous s'est posé(e) cette question. Tout au moins du temps de son adolescence.
En feuilletant d'anciennes notes de cours (mathématiques pur sucre), je retrouve une proposition de test très simple à effectuer sur votre personne.
Pour savoir si vous avez les proportions d'un Apollon, procédez ainsi :

calculer le rapport	distance sol à nombril/distance nombril à tête
et aussi	votre hauteur/distance sol à nombril

Plus le résultat de ces deux calculs sera proche de 1,618...., mieux vous serez proportionné. Je dois, sans fausse modestie, avouer que ce test me semble très valable...
Par contre, je n'ai rien à proposer pour le tour de taille.

Eh oui! Cette fameuse valeur 1,618 doit rappeler des souvenirs à ceux qui ont eu à se débattre avec la suite de Fibonacci (un vieil ami). Il s'agit bien là de ce fumeux 'nombre d'or'.
Alors, remontons un peu (4ème-3ème siècle av. JC) aux origines.
Ce cher Euclide, autre ami, chercha à établir "le partage en extrême et moyenne raison". Les explications mathématiques, inévitables à ce niveau, nous apprennent qu'il s'agit de déterminer un point I d'un segment [A,B] tel que :
^AI/_IB = ^AB/_AI , soit de façon graphique :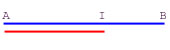

Pour en terminer avec ce laborieux aspect, je vous en rappelle la formule exacte, soit NombreOr = , et que ses propriétés mathématiques sont certainement remarquables.

Et Euclide s'en tiendra à cette théorie, sans aucune application pratique.
Ce n'est finalement qu'au XIXè siècle, qu'un professeur de philosophie, Adolf ZEISING, élabora une théorie sur l'esthétique des objets beaux et utilisa le terme de section d'or pour désigner ce rapport. Et ainsi naquit le 'Nombre d'or'.
Puis vers 1930, le Roumain Matila Ghyka voit du nombre d'or partout: les spirales des coquillages, la disposition des feuilles des plantes, le nombre de pétales,...Et aussi dans les oeuvres d'art, vases anciens, peinture, le Parthénon, etc. C'est à se demander s'il suffit de savoir ce que l'on cherche pour le trouver; ou de fixer les hypothèses de façon à pouvoir atteindre son but.
En ce qui concerne le Parthénon par exemple, d'autres études ont démontré que les Grecs s'en tenaient à des nombres entiers et ont relevé entre autres que la largeur de la façade correspondait au triple de la hauteur d'une colonne.
Et Dame Nature a certainement son mot à dire sur la disposition et le nombre de fleurons du tournesol (ou des écailles de pommes de pin ou d'ananas)...D'ailleurs les observations se référant au nombre d'or pour ces plantes émanent plutôt de physiciens que de botanistes.

De quoi constituer un véritable mythe; mais uniquement un mythe?
En regardant de plus près, on pourra noter que la glorification de la géométrie grecque par Matila Ghyka a comme corollaire la suprématie technique de la race blanche (in "rites et rythmes pythagoriens dans le développement de la civilisation occidentale"); discours qui me semble bien éloigné de nos chères mathématiques.
Etait-ce là CQFD ?

Il n'y a plus qu'à espérer que les indices de popularité de certains groupuscules, sans doute prompts à s'attribuer ce genre de thèses, suivent une évolution parallèle à celles des termes de la suite de Fibonacci de façon décroissante... Et rendons aux mathématiques, ce qui n'est que mathématiques.

Bibliographie

Marguerite Neveux, Le nombre d'or : radiographie d'un mythe. Coll. Points Sciences. Le Seuil
Matila Ghyka, Esthétique des proportions dans la nature et dans les arts. Le nombre d'or. Gallimard